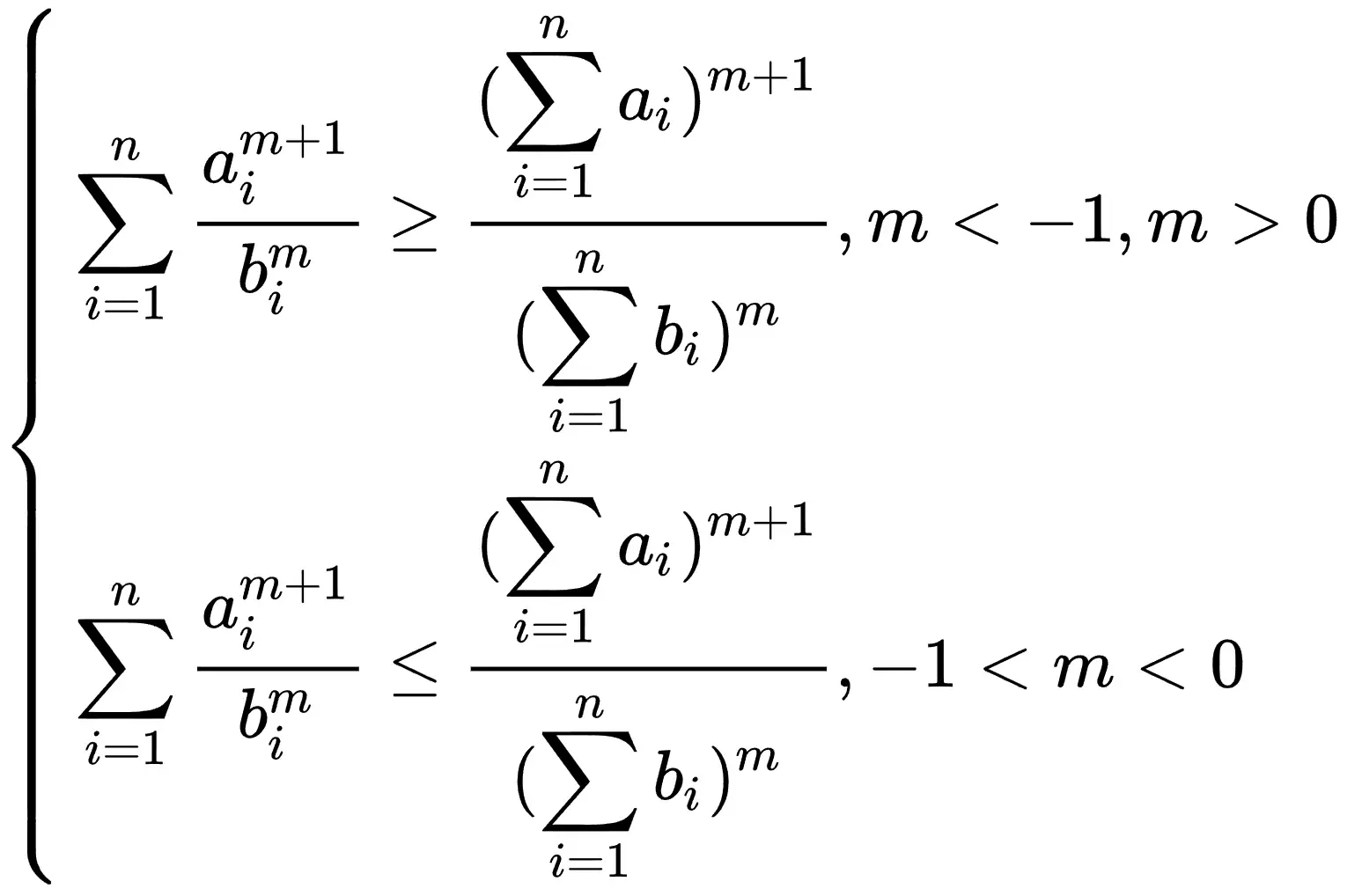本文极为简略,仅作为学习笔记使用,许多证明步骤未写出.
均值不等式
2a+b≥ab
这是高中数学课本上第一个重要的不等式,A 版教材称为基本不等式,B 版教材称为均值不等式.
其中,2a+b 称为算术平均值,ab 称为几何平均值.
证明
画图中……
变形
均值不等式有多个变形 / 推广形式,极其常用的有:
a+b≥2ab (a,b∈R+)
ab≤(2a+b)2 (a,b∈R+)
此外还有:
a+a1≥2 (a>0)
ba+ab≥2 (ba>0)
a2+b2≥2ab (a,b∈R)
应用
均值不等式的应用有三个条件:
- 一正: 两个数均为正实数,即 a,b∈R+.
- 二定: 求和时积为定值,求积时和为定值.
- 三相等: 等号能成立,即等号成立的条件能满足.
特殊情况:
一不正
条件一正没有满足即为一不正,又分为两种情况:
一不正
a,b 一正一负,即 a>0,b<0.
一不正时,均值不等式不成立,无法利用均值不等式求解.此时应放弃均值不等式,尝试将原式化为 f(x)=x−xp (p>0) 的形式.此函数为飘带函数,随后便可以利用函数的单调性求解.

二不正
a,b 均为负实数,即 a,b<0.
类似的,此时均值不等式不成立,无法利用均值不等式求解.此时应放弃均值不等式,提取 a,b 的负号,利用均值不等式求解之后,再利用不等式的基本性质二恢复负号.
二不定
条件二定没有满足即为二不定.此时均值不等式不成立,无法利用均值不等式求解主要利用配凑的方法求解.又分为两种情况:
求和积不定
利用加减等方法凑出分母的倍数.
例:当 x>1 时,求 x+x−14 的最小值.
将 x+x−14 转化为 (x−1)+x−14+1.检验 x−1>0 且 x−14>0 ,则有:
(x−1)+x−14+1≥2(x−1)⋅x−14+1=24+1=5
当且仅当 x−1=x−14,即 x=3 时,等号可以成立,得出 x+x−14 的最小值为 5.
求积和不定
改变某一因式系数使和为定值.
例:当 x∈(0,1) 时,求 x(3−2x) 的最大值.
将 x(3−2x) 转化为 21⋅2x(3−2x).检验 2x>0 且 x3−2x>0 ,则有:
21⋅2x(3−2x)≤21⋅[22x+(3−2x)]2=21⋅49=89
当且仅当 2x=3−2x,即 x=43 时,等号可以成立,得出 x(3−2x) 的最大值为 98.
三不相等
此时均值不等式不成立,无法利用均值不等式求解.此时应放弃均值不等式,尝试将原式化为 f(x)=x+xp (p>0) 的形式.此函数为对勾函数,其两个拐点一正一负,横坐标为 p 和 −p,代入求值得出拐点坐标后便可以利用函数的单调性求解.

1 的代换
1 的代换法是将代数式同时乘以 “1”,转化为均值不等式求解,通常是给出一个和,再求一个和的形式.
例:正数 x,y 满足 x3+y1=5,求 3x+4y 的最小值.
3x+4y=1⋅(3x+4y)=51⋅(x3+y1)⋅(3x+4y)=51⋅(x3⋅3x+x3⋅4y+y1⋅3x+y1⋅4y)=51(9+x12y+y3x+4)≥51⋅(9+4+2x12y⋅y3x)=51(9+4+12)=5
当且仅当 x12y=y3x 时,等号成立.联立方程:
{x3+y1=5x12y=y3x
解得:
{x=1y=21
满足条件,可得 3x+4y 的最小值为 5.
重要不等式
证明
由平方差公式:(a−b)2=a2−2ab+b2
并平方的性质:x2≥0
可以得到:a2−2ab+b2≥0
移项即可得:a2+b2≥2ab
可作为均值不等式的补充.
由于平方的性质中 x∈R,因此重要不等式的条件略有不同:
- 一实: 两个数均为实数,即 a,b∈R.
- 二定: 求和时积为定值,求积时和为定值.
- 三相等: 等号能成立,即等号成立的条件能满足.
连续不等式
均值不等式的全部如下:
a11+a21+⋯+an1n≤na1⋅a2⋯an≤na1+a2+⋯+an≤na12+a22+⋯+an2,其中:
a11+a21+⋯+an1n 是调和平均值,
na1⋅a2⋯an 是几何平均值,
na1+a2+⋯+an 是算术平均值,
na12+a22+⋯+an2 是平方平均值.
这个不等式链展示了不同平均值之间的大小关系.
糖水不等式
一杯质量为 b 的糖水含有质量为 a 的糖分,易得该杯糖的质量浓度为 ba.向杯中加入质量为 c 的糖,易得该杯糖水的质量浓度为 b+ca+c.由常识即可得 ba<b+ca+c.并由情境得:a>b>0,c>0.
证明
作差:ba−b+ca+c
简化后得到:b(b+c)c(a−b)>0
所以不等式 ba<b+ca+c 在 a>b>0,c>0 时成立.
权方和不等式
ax2+by2≥a+bx2+y2 (a,b,x,y∈R+)
证明
(ax2+by2)⋅(a+b)=x2+abx2+bay2+y2≥x2+y2+2abx2⋅bay2=x2+y2+2xy=(x+y)2
利用不等式的基本性质二即可得到 ax2+by2≥a+bx2+y2